LCG를 활용한 ID 셔플링
단일 데이터베이스를 쓸 경우 무난하게 사용할 수 있는 ID 생성 방식은 순차적으로 오르는 ID 를 사용하는 것이다. 이 방식의 아쉬운 점은 이전, 이후 id 가 유추가 가능하다는 것이다.
이럴 때, 오늘 알아볼 LCG를 활용한 ID 셔플링을 활용하면 간단한 알고리즘으로 좀 더 데이터를 은닉할 수 있게 된다. (아래에서 설명하겠지만 완벽한 보안을 보장하는 것이 아니다.)
LCG란 무엇인가?
LCG(Linear Congruential Generator, 선형 합동 생성기)는 의사난수(pseudo-random number)를 생성하는 알고리즘 중 하나이다. 가장 오래되고 널리 알려진 PRNG(Pseudo-Random Number Generator) 중 하나이다.
“의사난수”라는 이름에서 알 수 있듯이, LCG는 진정한 난수가 아닌 결정론적(deterministic) 방식으로 난수처럼 보이는 수열을 생성한다. 동일한 시드(seed) 값을 사용하면 항상 동일한 수열이 생성된다.
LCG의 수학적 원리
원리는 간단한 편이다.
LCG는 다음과 같은 점화식(recurrence relation)을 사용한다:
\[X_{n+1} = (a \cdot X_n + c) \mod m\]각 변수의 의미는 다음과 같다:
| 변수 | 이름 | 설명 |
|---|---|---|
| $X_n$ | 현재 값 | 현재 난수 값 |
| $X_{n+1}$ | 다음 값 | 생성될 다음 난수 값 |
| $a$ | 승수(multiplier) | 곱해지는 상수 |
| $c$ | 증분(increment) | 더해지는 상수 |
| $m$ | 모듈러(modulus) | 나머지 연산에 사용되는 값 |
| $X_0$ | 시드(seed) | 초기값 |
작동 예시
간단한 예시로 LCG가 어떻게 동작하는지 살펴보자.
- $a = 5$, $c = 3$, $m = 16$, $X_0 = 7$ 로 설정하면:
| n | 계산 과정 | $X_n$ |
|---|---|---|
| 0 | 초기값 | 7 |
| 1 | $(5 \times 7 + 3) \mod 16 = 38 \mod 16$ | 6 |
| 2 | $(5 \times 6 + 3) \mod 16 = 33 \mod 16$ | 1 |
| 3 | $(5 \times 1 + 3) \mod 16 = 8 \mod 16$ | 8 |
| 4 | $(5 \times 8 + 3) \mod 16 = 43 \mod 16$ | 11 |
이런 식으로 연속적인 난수 수열이 생성된다.
좋은 파라미터 선택 기준
LCG 를 사용할 때에는 적절한 파라미터(a, c, m) 선택이 중요하다.
주기(Period)란?
LCG는 모듈러 연산을 사용하기 때문에 생성되는 수열은 결국 반복된다. 주기(period)란 수열이 반복되기 전까지 생성되는 서로 다른 값의 개수를 말한다.
예를 들어, 위의 예시($a = 5$, $c = 3$, $m = 16$)에서 수열을 계속 생성하면 어느 순간 이전에 나왔던 값이 다시 나타나고, 그 이후로는 같은 패턴이 반복된다.
최대 주기(full period)
최대 주기는 가능한 모든 값(0부터 $m-1$까지)이 한 번씩 나타나는 것을 의미한다. 즉, 주기가 $m$과 같을 때 최대 주기를 갖는다고 한다. 최대 주기를 가지면 생성되는 난수가 가장 균등하게 분포되므로, 좋은 LCG는 최대 주기를 갖도록 파라미터를 선택해야 한다.
최대 주기를 위한 조건(Hull-Dobell 정리)
최대 주기를 얻기 위해서는 다음 조건을 모두 만족해야 한다:
- $c$와 $m$은 서로소(coprime)이어야 한다
- $a - 1$은 $m$의 모든 소인수로 나누어 떨어져야 한다
- $m$이 4의 배수이면, $a - 1$도 4의 배수여야 한다
실제 사용되는 파라미터 예시
| 사용처 | $m$ | $a$ | $c$ |
|---|---|---|---|
| glibc | $2^{31}$ | 1103515245 | 12345 |
| Microsoft Visual C++ | $2^{32}$ | 214013 | 2531011 |
| MINSTD | $2^{31} - 1$ | 48271 | 0 |
더 많은 파라미터 예시는 LCG#Parameters in common use 에서 확인해볼 수 있다.
ID 셔플 함수로 활용하기
LCG 에 대해 알아보았으니 본격적으로 오늘 다뤄보고자 한 ID 셔플링에 대해 설명해보겠다.
원래 LCG는 이전 결과값을 다음 입력으로 사용하여 수열을 만드는 용도이다. 하지만 LCG의 수식을 빌려와 순차적 ID를 셔플(shuffle)하는 함수로 활용할 수도 있다.
\[f(id) = (a \cdot id + c) \mod m\]이 방식은 순차적으로 증가하는 ID($0, 1, 2, 3, \ldots$)를 입력으로 넣어 난수처럼 보이는 값으로 변환한다:
\[f(0), f(1), f(2), f(3), \ldots\]참고: 이는 LCG 수열의 n번째 항을 직접 계산하는 것과는 다르다. 여기서는 단순히 LCG의 선형 변환 수식을 ID 셔플 용도로 활용하는 것이다.
구현 예시
Java
public class LCG {
private final long a;
private final long c;
private final long m;
public LCG(long a, long c, long m) {
this.a = a;
this.c = c;
this.m = m;
}
// 직접 접근 방식: ID를 입력받아 변환된 값을 반환
public long transform(long id) {
return (a * id + c) % m;
}
public static void main(String[] args) {
// glibc 파라미터 사용
LCG lcg = new LCG(1103515245, 12345, (1L << 31));
// 순차 ID(0, 1, 2, ...)를 난수처럼 보이는 값으로 변환
for (int i = 0; i < 10; i++) {
System.out.printf("ID %d -> %d%n", i, lcg.transform(i));
}
}
}
실행 결과
ID 0 -> 12345
ID 1 -> 1103527590
ID 2 -> 59559187
ID 3 -> 1163074432
ID 4 -> 119106029
ID 5 -> 1222621274
ID 6 -> 178652871
ID 7 -> 1282168116
ID 8 -> 238199713
ID 9 -> 1341714958
Base34 변환
여기서 조금 더 난수처럼 보이고 싶다면 Base34 인코딩을 활용할 수 있다. Base34는 0-9(10개)와 A-Z에서 I, O를 제외한 24개 문자를 사용하여 총 34개의 문자로 숫자를 표현하는 방식이다.
Base34 에서
I는 숫자1과,O는 숫자0과 혼동되기 쉬워 제외한다.
변환 원리
10진수를 34진법으로 변환하는 과정은 다음과 같다:
- 숫자를 34로 나눈 나머지를 구한다
- 나머지에 해당하는 문자를 기록한다
- 몫이 0이 될 때까지 반복한다
- 기록한 문자를 역순으로 나열한다
구현 예시
Java
public class Base34 {
private static final String CHARACTERS = "0123456789ABCDEFGHJKLMNPQRSTUVWXYZ";
// I, O 제외 (혼동 방지)
public static String encode(long number) {
if (number == 0) return "0";
StringBuilder result = new StringBuilder();
while (number > 0) {
int remainder = (int) (number % 34);
result.append(CHARACTERS.charAt(remainder));
number /= 34;
}
return result.reverse().toString();
}
public static long decode(String encoded) {
long result = 0;
for (char c : encoded.toCharArray()) {
result = result * 34 + CHARACTERS.indexOf(c);
}
return result;
}
public static void main(String[] args) {
LCG lcg = new LCG(1103515245, 12345, (1L << 31));
// 순차 ID를 LCG로 변환 후 Base34 인코딩
for (int i = 0; i < 10; i++) {
long value = lcg.transform(i);
String encoded = encode(value);
System.out.printf("ID %d -> %d -> %s%n", i, value, encoded);
}
}
}
출력 예시
ID 0 -> 12345 -> AP3
ID 1 -> 1103527590 -> Q9SQMU
ID 2 -> 59559187 -> 1AKBST
ID 3 -> 1163074432 -> RLBRRJ
ID 4 -> 119106029 -> 2M4CWH
ID 5 -> 1222621274 -> SWWSV8
ID 6 -> 178652871 -> 3XPE07
ID 7 -> 1282168116 -> U7FTYY
ID 8 -> 238199713 -> 588F3X
ID 9 -> 1341714958 -> VJ0V2N
활용 예시
Base34로 인코딩된 LCG 출력은 다음과 같은 용도로 활용할 수 있다:
- 단축 URL 생성: 긴 숫자 ID를 짧은 문자열로 변환
- 고유 코드 생성: 쿠폰 코드, 초대 코드 등
- 파일명 생성: 임시 파일이나 업로드 파일의 고유 이름
LCG의 장점과 단점
장점
- 빠른 속도: 단순한 산술 연산만 사용하므로 매우 빠르다
- 적은 메모리: 현재 상태 값 하나만 저장하면 된다
- 재현 가능성: 동일한 시드를 사용하면 동일한 수열을 재현할 수 있다
- 구현 용이: 알고리즘이 단순하여 구현하기 쉽다
단점
- 예측 가능성: 연속된 몇 개의 값만 알면 전체 수열을 예측할 수 있다
- 낮은 차원에서의 상관관계: 연속된 값들을 n차원 공간에 점으로 찍으면 초평면(hyperplane) 위에 놓이는 특성이 있다 (Marsaglia의 정리)
- 제한된 주기: 최대 주기가 $m$으로 제한된다
사용 시 주의사항
보안 목적으로 사용하면 안 된다
LCG는 암호학적으로 안전하지 않다(cryptographically insecure). 단순히 숫자가 커졌다 작아졌다 하는 착시를 줄 뿐, 패턴 분석에 매우 취약하다.
LCG는 선형성이 강하기 때문에, $a$와 $c$ 값을 모르더라도 몇 개의 (입력, 출력) 쌍만 알면 간단한 연립방정식으로 파라미터를 알아낼 수 있다. 실제 보안이 필요한 곳에서는 절대 사용하면 안 된다.
보안이 필요한 경우 CSPRNG(Cryptographically Secure PRNG)를 사용해야 한다. Java에서는 SecureRandom이 이를 제공한다.
마무리
LCG는 단순하면서도 효과적인 의사난수 생성 알고리즘이다. 알아두면 유용하게 사용할 수 있을 것이다.
참고
최대 주기 실제로 확인해보기
간단한 예시로 최대 주기가 실제로 어떻게 만들어지는지 확인해보겠다.
$m = 8$, $a = 5$, $c = 1$로 설정하면 위에서 설명한 Hull-Dobell 조건을 모두 만족한다:
- $c = 1$과 $m = 8$은 서로소 ✓
- $a - 1 = 4$는 $m$의 소인수 2로 나누어 떨어짐 ✓
- $m = 8$이 4의 배수이고, $a - 1 = 4$도 4의 배수 ✓
$X_0 = 0$부터 시작하여 수열을 생성하면 다음과 같이 나온다.
| n | 계산 과정 | $X_n$ |
|---|---|---|
| 0 | 초기값 | 0 |
| 1 | $(5 \times 0 + 1) \mod 8 = 1$ | 1 |
| 2 | $(5 \times 1 + 1) \mod 8 = 6$ | 6 |
| 3 | $(5 \times 6 + 1) \mod 8 = 31 \mod 8$ | 7 |
| 4 | $(5 \times 7 + 1) \mod 8 = 36 \mod 8$ | 4 |
| 5 | $(5 \times 4 + 1) \mod 8 = 21 \mod 8$ | 5 |
| 6 | $(5 \times 5 + 1) \mod 8 = 26 \mod 8$ | 2 |
| 7 | $(5 \times 2 + 1) \mod 8 = 11 \mod 8$ | 3 |
| 8 | $(5 \times 3 + 1) \mod 8 = 16 \mod 8$ | 0 |
8번째 단계에서 다시 0으로 돌아왔다. 생성된 수열 0 → 1 → 6 → 7 → 4 → 5 → 2 → 3 → 0을 보면, 0부터 7까지 모든 값이 정확히 한 번씩 나타난 후 다시 처음으로 돌아온다.
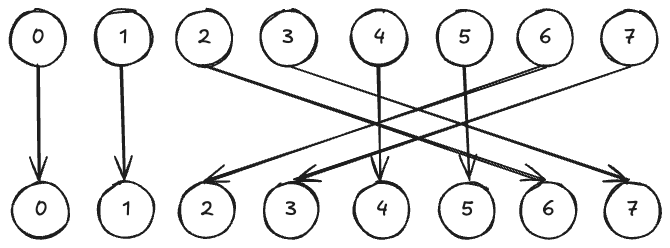
이것이 바로 최대 주기($m = 8$)를 갖는 LCG의 특성이다.