트리 알아보기 - 이진 트리, 이진 탐색 트리, AVL 트리, B-트리, B+트리, Red Black 트리
지난 2월 17일 K-DEVCON 대전 스터디에서 공유한 내용을 블로그에도 정리해본다.
최근에 알고리즘 문제를 하루에 한 개 이상씩 풀려고 하는 중인데, 마침 B 트리와 관련된 내용을 다루게 되어서 트리 종류들을 간단하게 정리해서 스터디에서 공유하였다.
이 자료는 다양한 트리에 대해 개략적으로 정리한 것이다. 또한 시간순으로 정렬해두었다.
더 구체적인 부분들이 궁금하다면 함께 달아놓은 링크나 검색을 통해 찾아보면 된다.
대부분의 내용/이미지는 위키피디아를 참조하였다.
Binary 트리 (이진 트리)
설명
- Binary Tree wiki
- 가장 기초적인 트리이다.
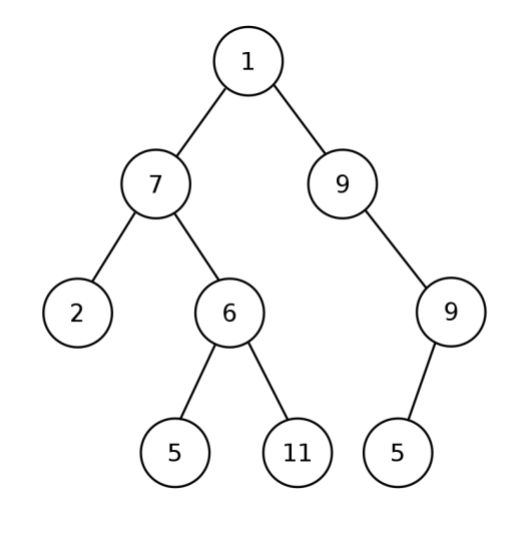
- 이진 트리는 각 노드에 최대 2개의 자식(왼쪽 자식 과 오른쪽 자식)이 있는 트리 데이터 구조 이다.
- 이전부터 있었고, 20세기 중반쯤 부터 컴퓨터 과학 논문들에서 언급되기 시작했다고 한다.
- 그냥 이진 트리를 이야기 할 때에는 삽입/삭제 규칙이 따로 없다.
- 아직 균형이 잡혀있는 구조는 아니다.
이미지
Binary Search 트리 (이진 검색 트리)
설명
- Binary Search Tree wiki
- 이진 트리의 일종이다. 약자만 따서 BST 라고도 한다.
- 규칙을 추가하였다.
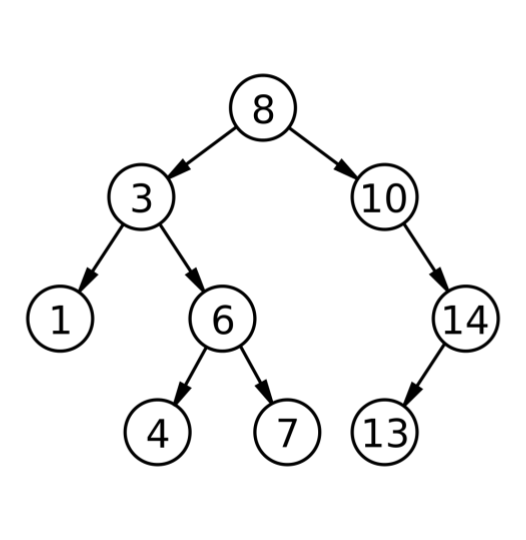
- 노드의 왼쪽 서브트리에는 그 노드의 값보다 작은 값들을 지닌 노드들로 이루어져 있다.
- 노드의 오른쪽 서브트리에는 그 노드의 값보다 큰 값들을 지닌 노드들로 이루어져 있다.
- 좌우 하위 트리는 각각이 다시 이진 탐색 트리여야 한다.
- 쉽게 정리하면 작으면 왼쪽으로, 크면 오른쪽으로 보낸다고 생각하면 된다.
- 아쉽게도 균형이 잡혀있는 구조는 아닐수도 있다.
- 1960년 발표
이미지
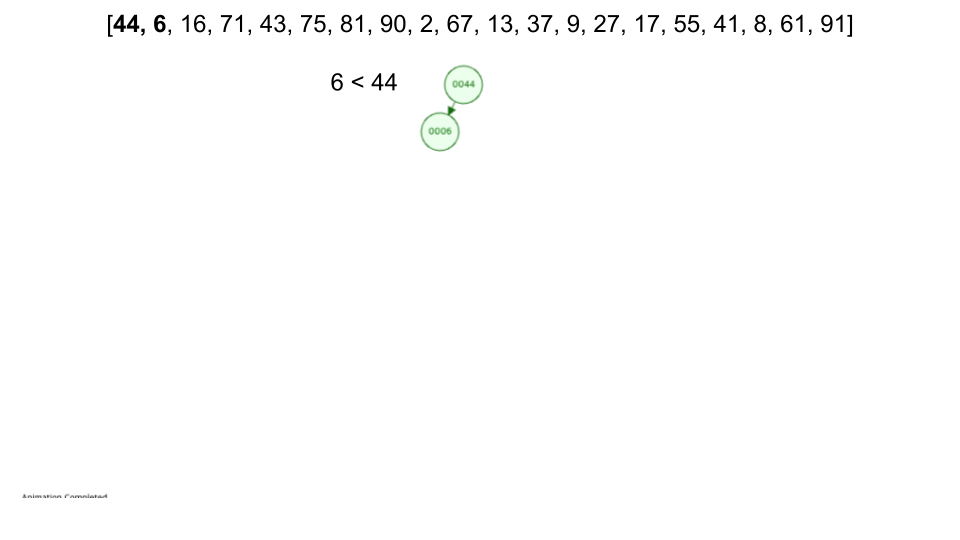
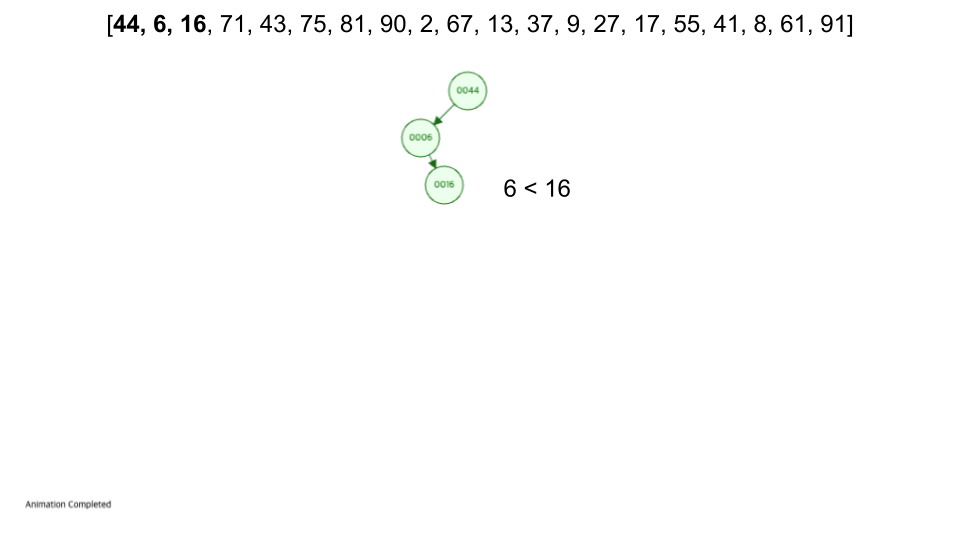
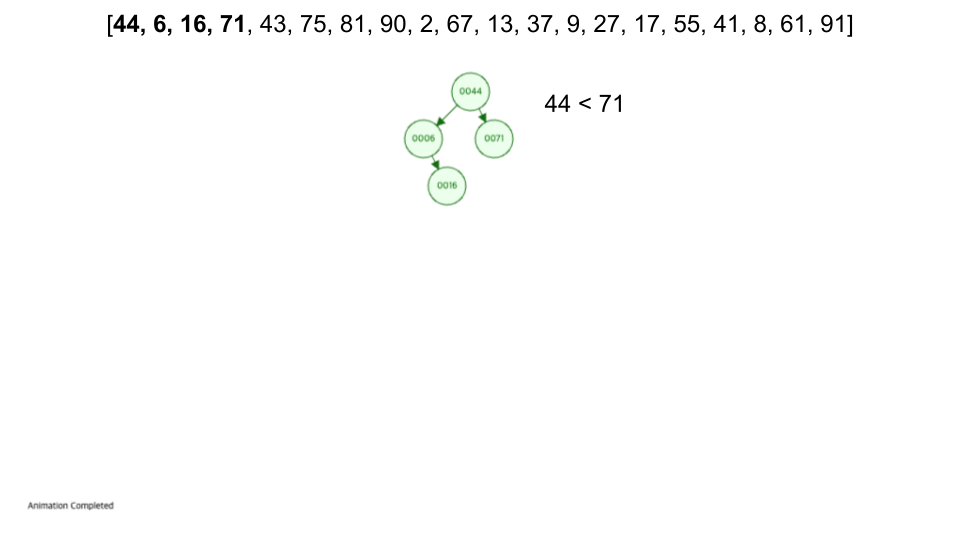
삽입 과정
- 루트(Root, 뿌리)에서 시작합니다.
- 삽입 값과 루트와 비교합니다.
- 루트보다 작으면 왼쪽으로 재귀하고 크다면 오른쪽으로 재귀합니다.
- 리프 노드(맨 끝)에 도달하였을 때, 해당 노드보다 작으면 왼쪽 크면 오른쪽에 삽입합니다.
- 따라서 어던 노드가 처음에 들어오냐가 중요합니다.
visualization
- https://www.cs.usfca.edu/~galles/visualization/BST.html
- 입력 순서 :
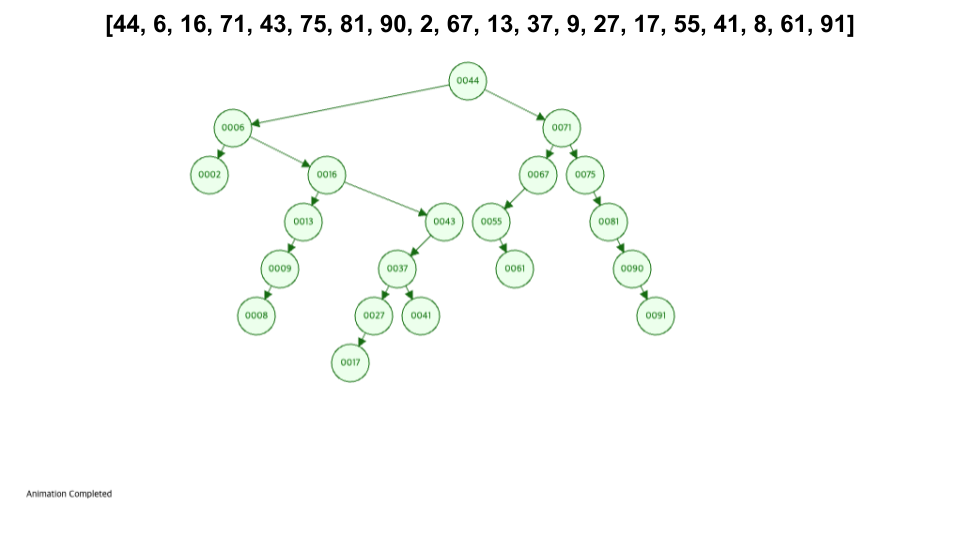
[44, 6, 16, 71, 43, 75, 81, 90, 2, 67, 13, 37, 9, 27, 17, 55, 41, 8, 61, 91]

삭제 과정
- 자식 노드가 없는 노드 일 경우
- 단순하게 해당 노드를 삭제한다.
- 자식 노드가 1개인 노드 삭제
- 해당 노드를 삭제하고 그 위치에 해당 노드의 자식 노드를 대입한다.
- 자식 노드가 2개인 노드 삭제
- 방법1: 삭제하고자 하는 노드의 값을 해당 노드의 왼쪽 서브트리에서 가장 큰값으로 변경한 뒤, 해당 노드를 삭제한다.
- 방법2: 삭제하고자 하는 노드의 값을 해당 노드의 오른쪽 서브트리에서 가장 작은 값으로 변경한 뒤, 해당 노드를 삭제한다.
성능
- 트리가 잘 균현이 잡혀있을 경우 평균 이상의 성능을 낸다.
- 한쪽으로 쏠려 있을 경우 최악의 성능을 낸다. (마치 linked list 같다.)
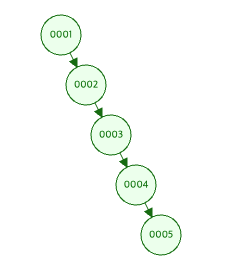
| 평균 | 최악 | |
|---|---|---|
| 조회 | O(logN) | O(N) |
| 삽입 | O(logN) | O(N) |
| 삭제 | O(logN) | O(N) |
| 공간복잡도 | O(N) | O(N) |
정리
- 이진 검색 트리의 삽입, 삭제 과정은 다른 트리들의 기본이 되므로 잘 기억해두면 좋다.
- BST의 단점은 균형이 맞지 않을 경우 성능이 잘 나오지 않는다는 것이였다. 이후의 트리들은 이 단점을 보완해서 나온다.
AVL 트리
설명
- AVL Tree wiki
- 자가 균형 이진 탐색 트리(self-balancing binary search tree)
- 기본적으로 이진 탐색 트리의 규칙을 따라가나 트리가 불균형 해질 경우 노드를 회전시켜 균형을 맞추는 것이 특징이다.
- 1962년 에 발표되었다.
- AVL은 발명자의 이름에서 따왔다. (따라서 특별한 의미는 없다.)
회전
- 균형을 맞추기 위해 회전(rotation) 개념이 추가되었다.
- 왼쪽의 높이와 오른쪽의 높이의 차이가 2만큼 난다면 rotation을 통해 균형(balance)를 맞춘다.
- rotate가 발생되었을 때는, 중앙에 중간값 노드가, 좌측에는 작은값 노드가, 우측에는 큰값 노드가 배치된다고 생각하면 된다.
회전이 발생하는 주요 모양
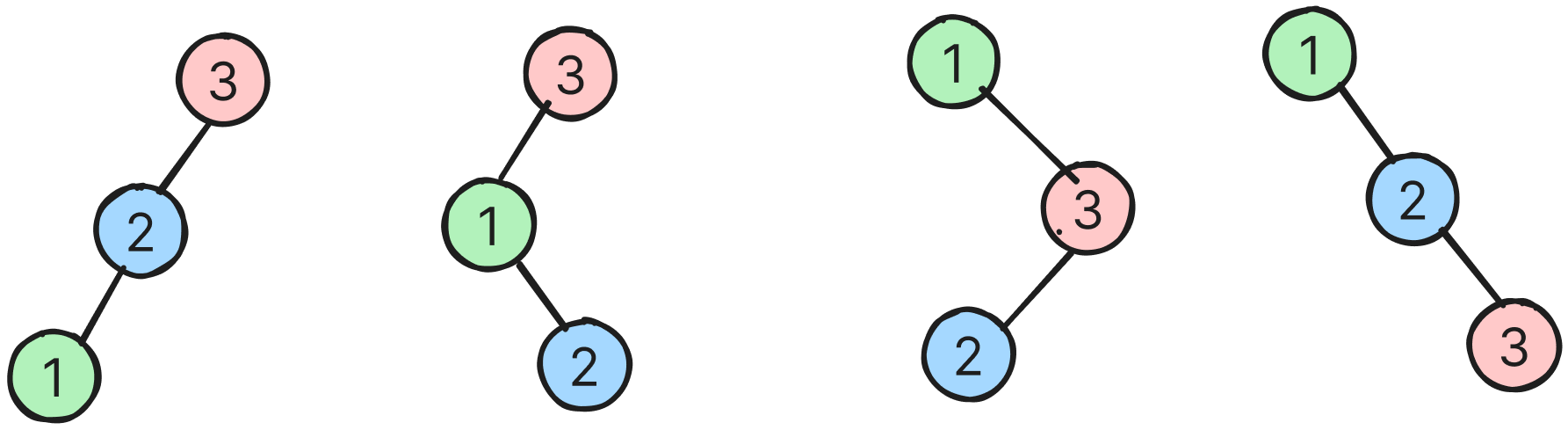
- 개인적으로 자료를 준비하면서 여러번 테스트 해보니 이러한 모양일 경우에 회전이 발생될 가능성이 높았다.
- 물론 이 외의 경우에도 발생한다. 따라서 참고만 해라.
visualization
- https://www.cs.usfca.edu/~galles/visualization/AVLtree.html
- 입력 순서 :
[44, 6, 16, 71, 43, 75, 81, 90, 2, 67, 13, 37, 9, 27, 17, 55, 41, 8, 61, 91]

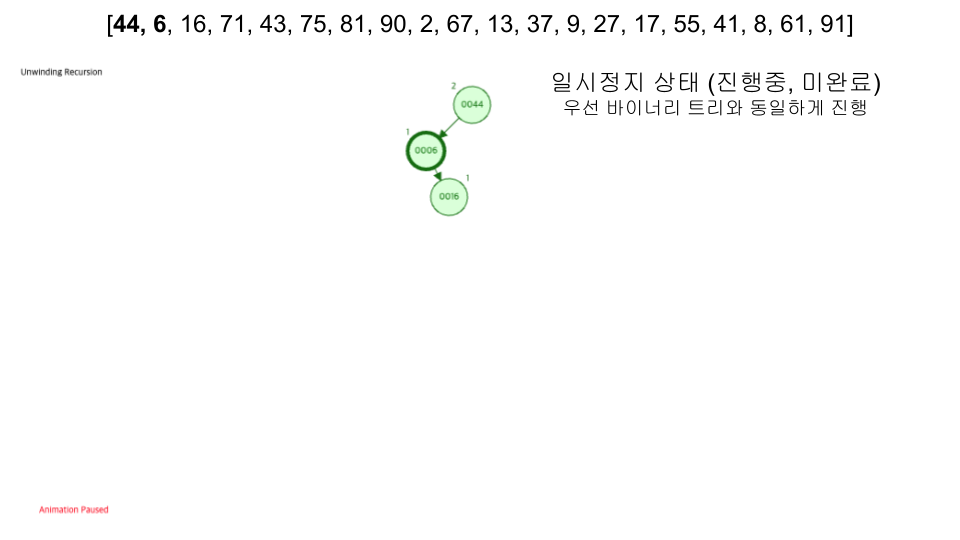

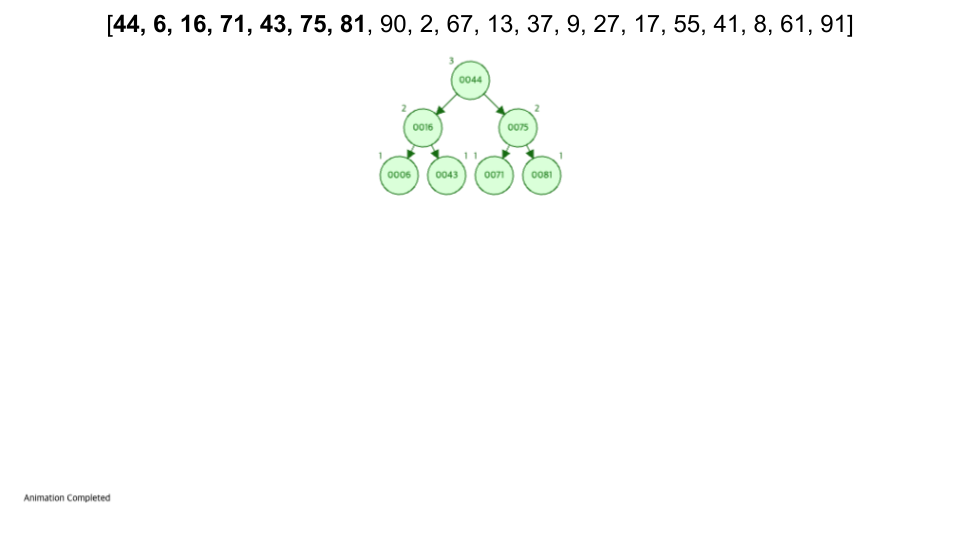
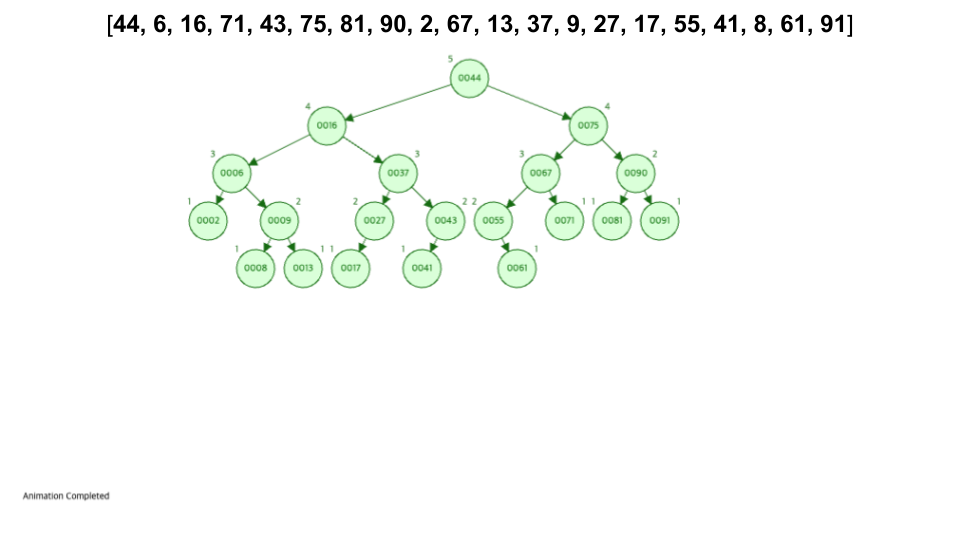
삭제과정
삽입 과정과 마찬가지로 이진 탐색 트리와 동이랗게 진행한 후 높이 차이가 발생되었을 때 회전을 진행해주면 된다.
B-Tree
어떻게 불러야 하는거지?
- 그냥 B(비) 트리라고 부르면 된다. B가 특별한 의미가 없다고 한다. (여러가지 설은 있지만)
- 비 마이너스 트리 라고 부르면 안된다. (B+ 트리가 있다보니, 나는 처음에 부끄럽게도 비 마이너스 트리인줄 알았다.)
설명
- B-tree wiki
- B-트리는 정렬된 데이터를 유지하는 자체 균형 트리(self-balancing tree) 이다.
- B-트리는 이진 검색 트리를 일반화하여 2개 이상의 자식을 가진 노드를 허용한다.
- 다른 자체 균형 이진 검색 트리와 달리 B-트리는 데이터베이스 및 파일 시스템 과 같이 비교적 큰 데이터 블록을 읽고 쓰는 저장 시스템에 매우 적합하다
- 1970년 발표되었다.
정의
Knuth 라는 사람이 세운 정의는 다음과 같다.
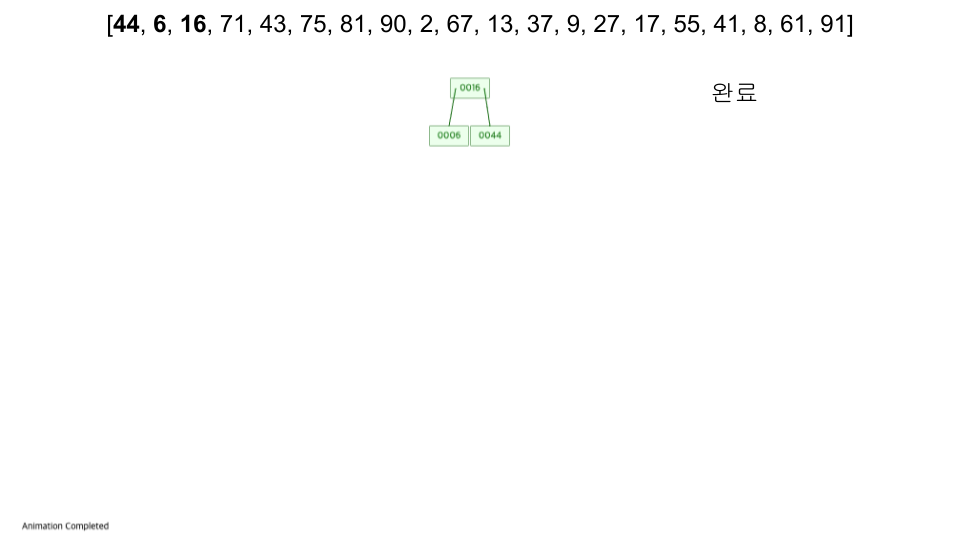
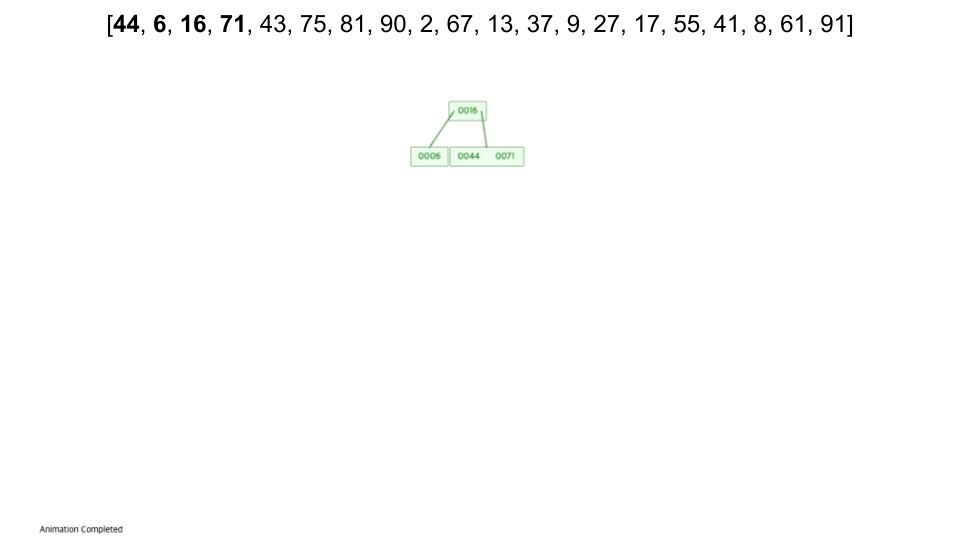
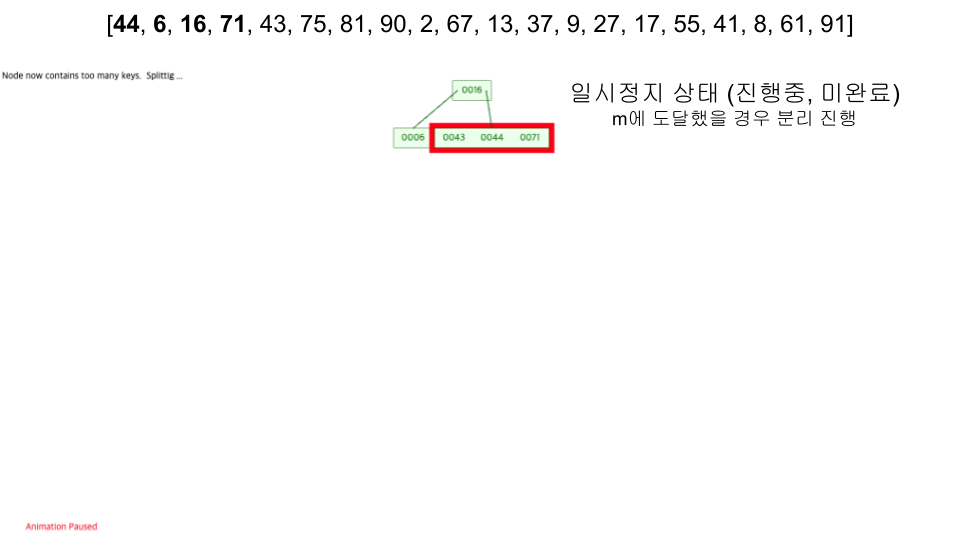
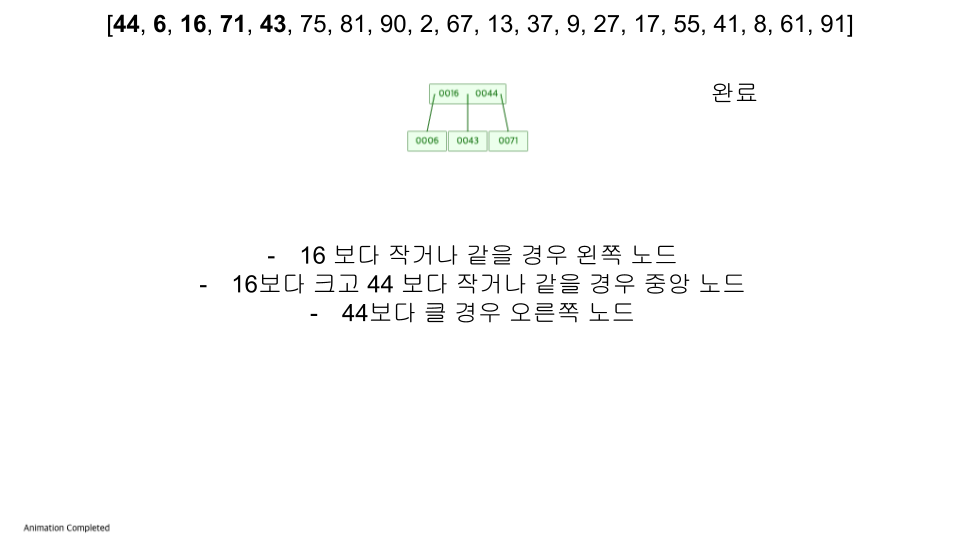
m 차의 B-트리는 (m은 3이상의 정수)
- 모든 노드에는 최대 m 개의 자식이 있습니다.
- 모든 내부 노드에는 최소 ⌈ m / 2 ⌉ 개의 하위 노드가 있습니다.
- 루트 노드는 리프가 아닌 한 최소한 두 개의 하위 노드를 갖습니다.
- 모든 리프 노드는 같은 수준에 나타납니다.
- k 개의 자식 이 있는 리프가 아닌 노드에는 k − 1 개의 키가 포함됩니다.
참고로
⌈ ⌉는 올림이라는 뜻이다.
visualization
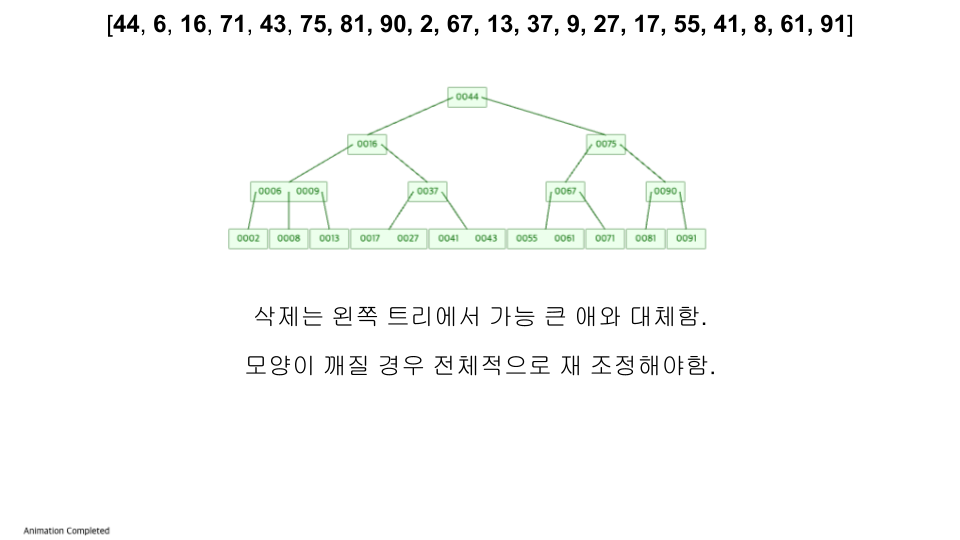
- https://www.cs.usfca.edu/~galles/visualization/BTree.html
- 입력 순서 :
[44, 6, 16, 71, 43, 75, 81, 90, 2, 67, 13, 37, 9, 27, 17, 55, 41, 8, 61, 91]



성능
| 평균 | 최악 | |
|---|---|---|
| 조회 | O(logN) | O(logN) |
| 삽입 | O(logN) | O(logN) |
| 삭제 | O(logN) | O(logN) |
| 공간복잡도 | O(N) | O(N) |
B+Tree
설명
- B+tree wiki
- 정식적으로 논문으로 발표된 것은 아니며 1973년에 IBM에서 사용하기 시작한 것으로 알려져 있다.
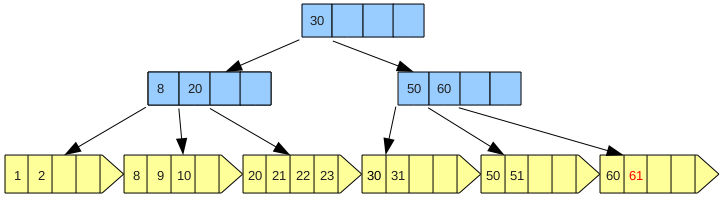
- 범위(range) 검색에 유리하다.
- 데이터가 모두 리프 노드에만 저장되는 것이 특징이다.
이미지
visualization
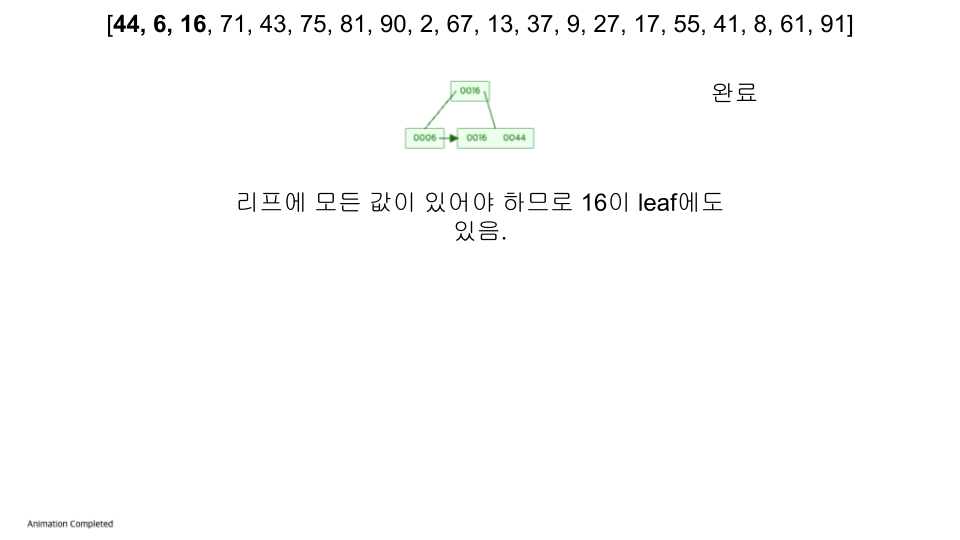
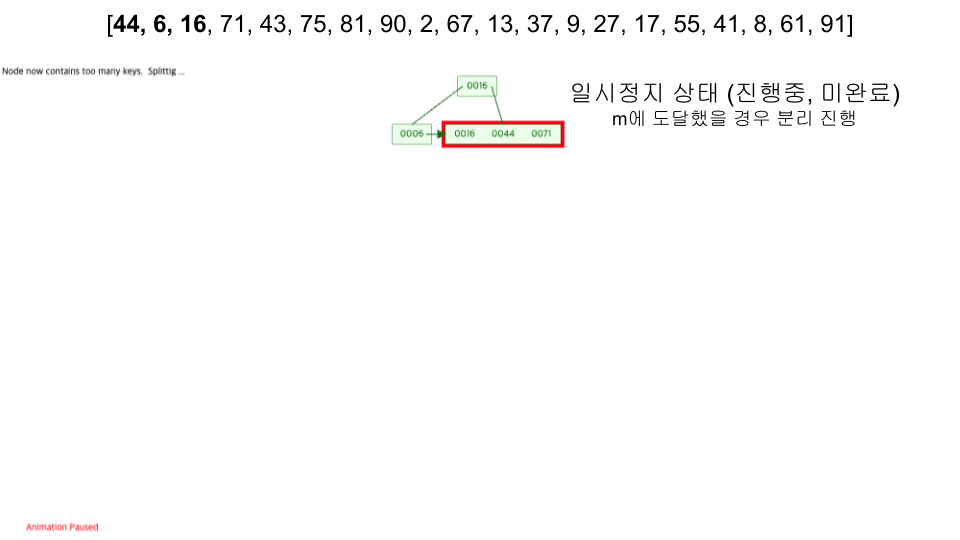
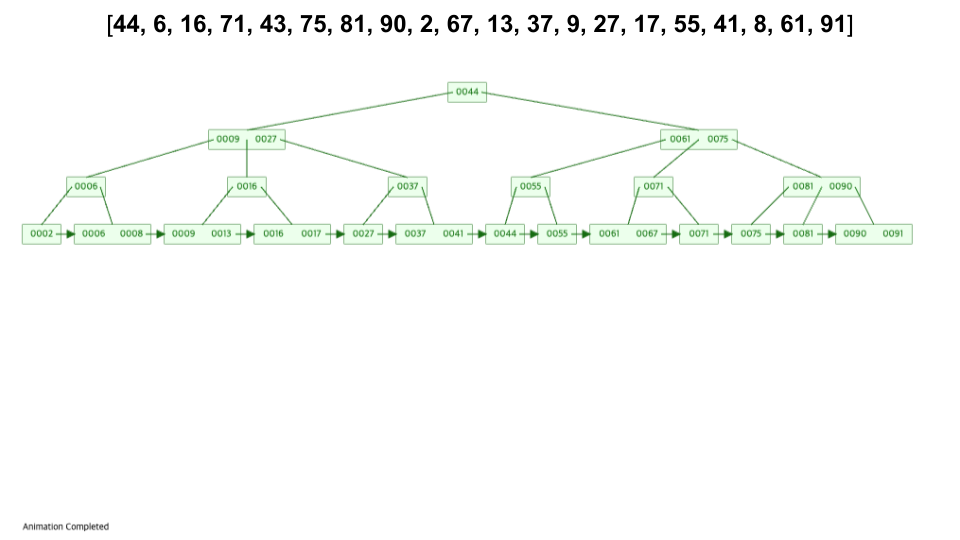
- https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html
- 입력 순서 :
[44, 6, 16, 71, 43, 75, 81, 90, 2, 67, 13, 37, 9, 27, 17, 55, 41, 8, 61, 91]



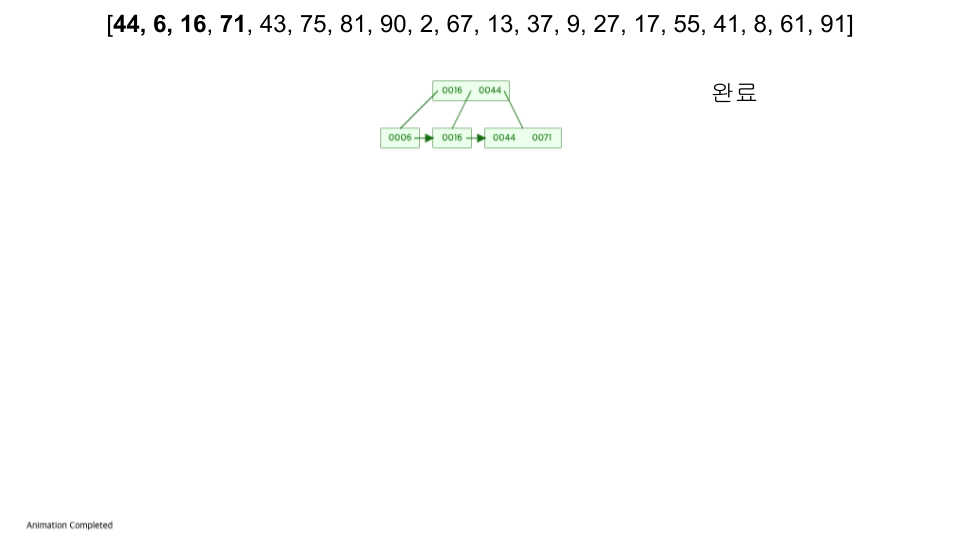
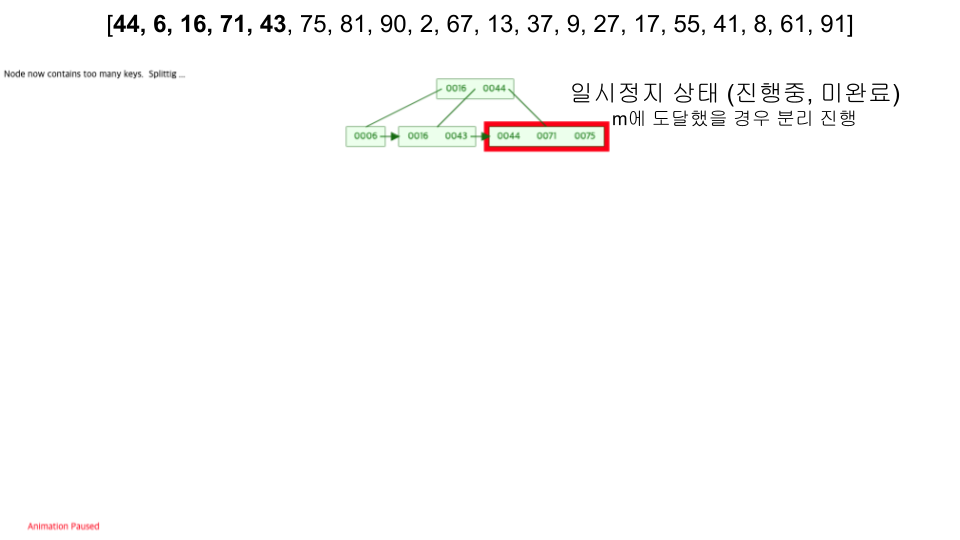
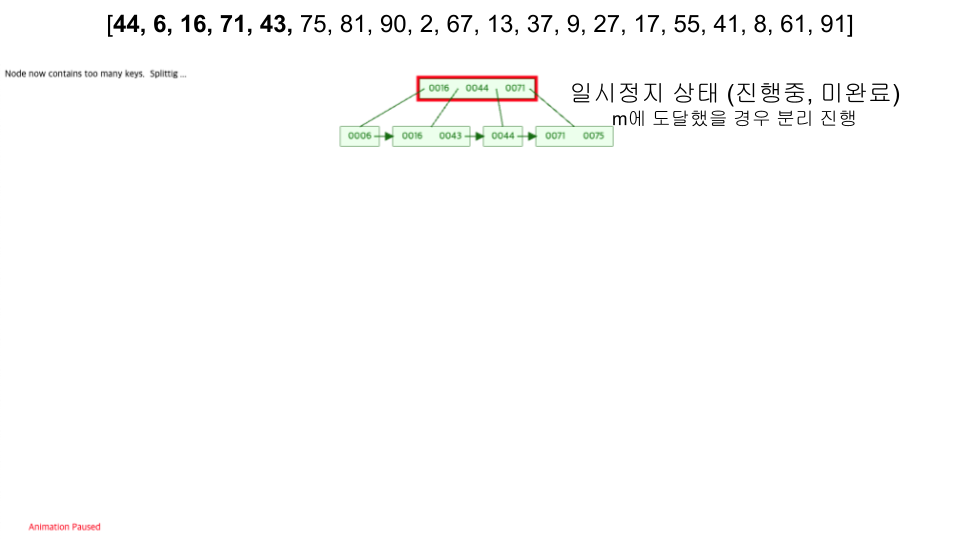
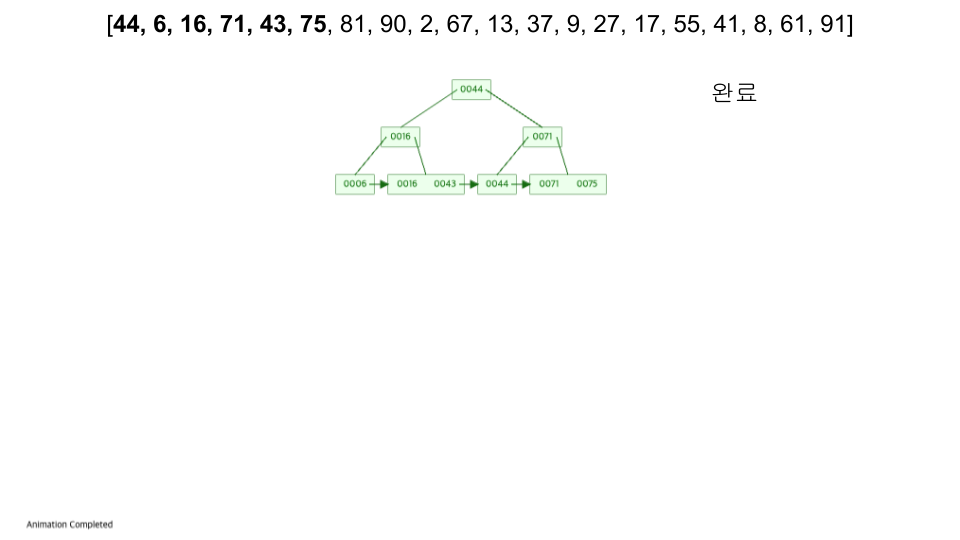
성능
| 평균 | 최악 | |
|---|---|---|
| 조회 | O(logN) | O(logN) |
| 삽입 | O(logN) | O(logN) |
| 삭제 | O(logN) | O(logN) |
| 공간복잡도 | O(N) | O(N) |
Red Black 트리
설명
- Red Black Tree wiki
- 자가 균형 이진 탐색 트리(self-balancing binary search tree)
- 구현은 꽤나 복잡하지만 실 사용에선 매우 효율적인 모습을 보인다.
- 1978년 발표
- 레드-블랙 트리는 색깔 속성을 이용하여 균형을 유지한다. (AVL 트리는 각 노드의 양쪽 서브트리의 높이 차이를 일정하게 유지하여 균형을 유지하였다.)
- 4차 B 트리와 비슷한 구조를 가진다고 한다.
- C++ STL의 set, map이 이 Red Black 트리를 이용하여 구현하였다고 한다.
이미지
트리의 속성
- 노드는 레드 혹은 블랙 중의 하나이다.
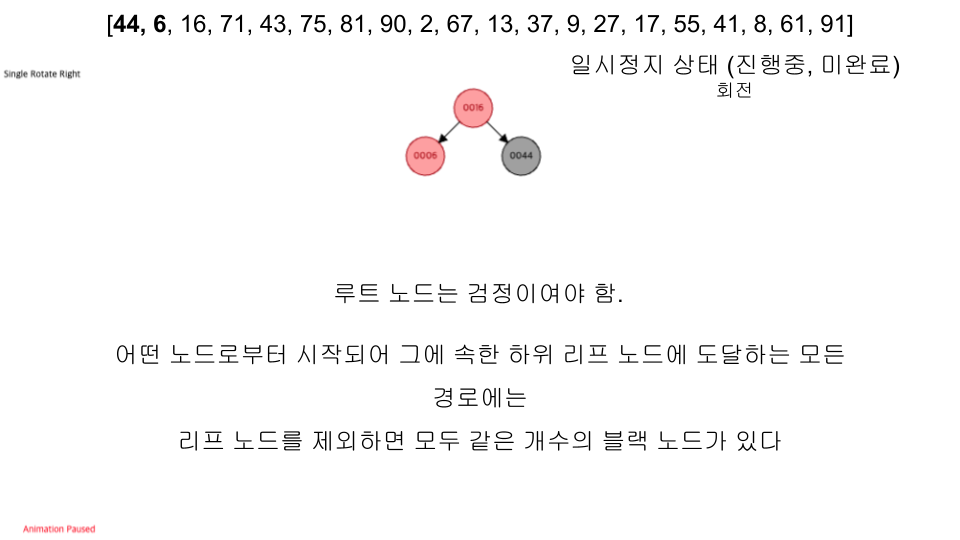
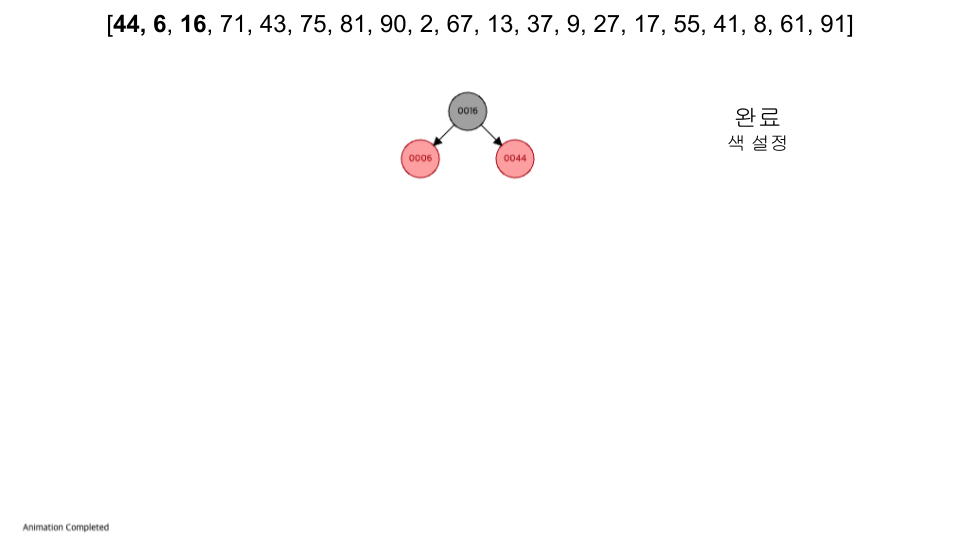
- 루트 노드는 블랙이다.
- 모든 리프 노드들(NIL)은 블랙이다.
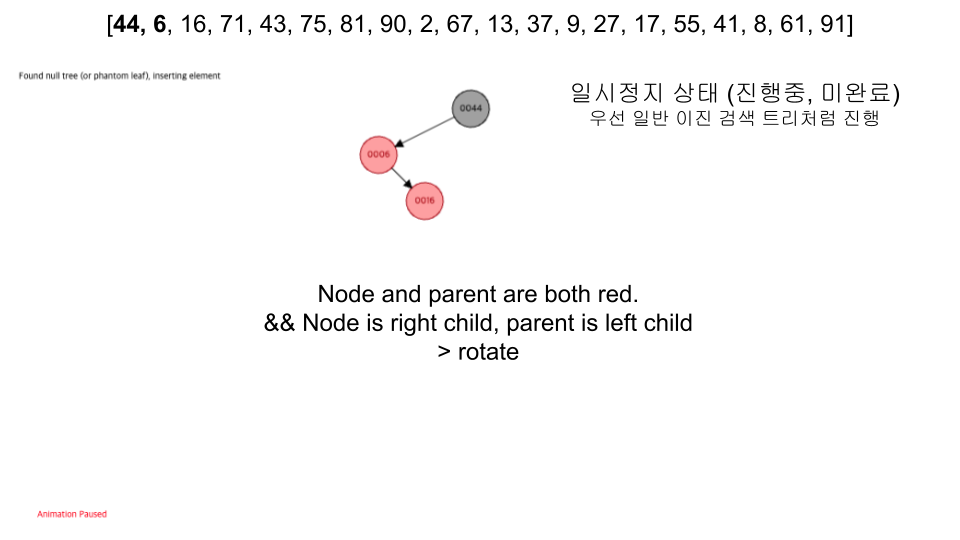
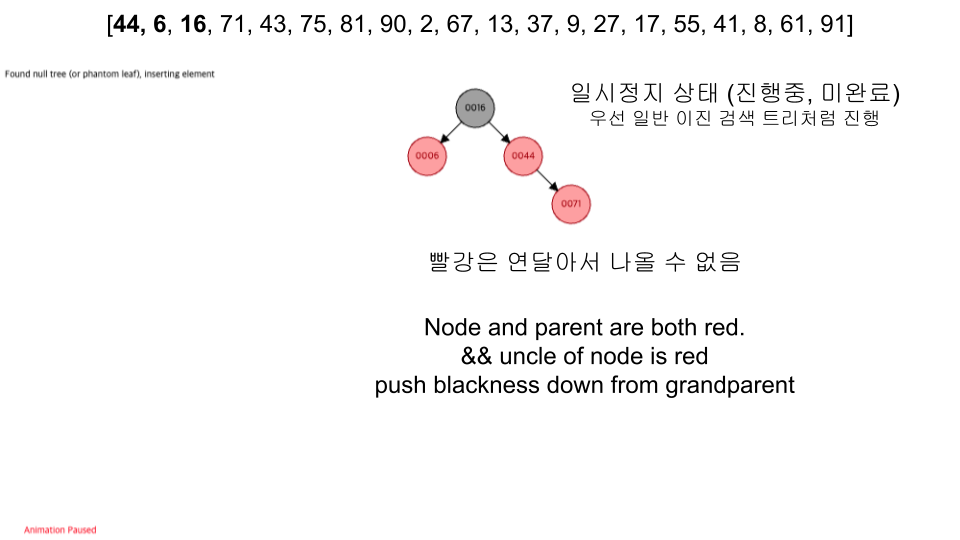
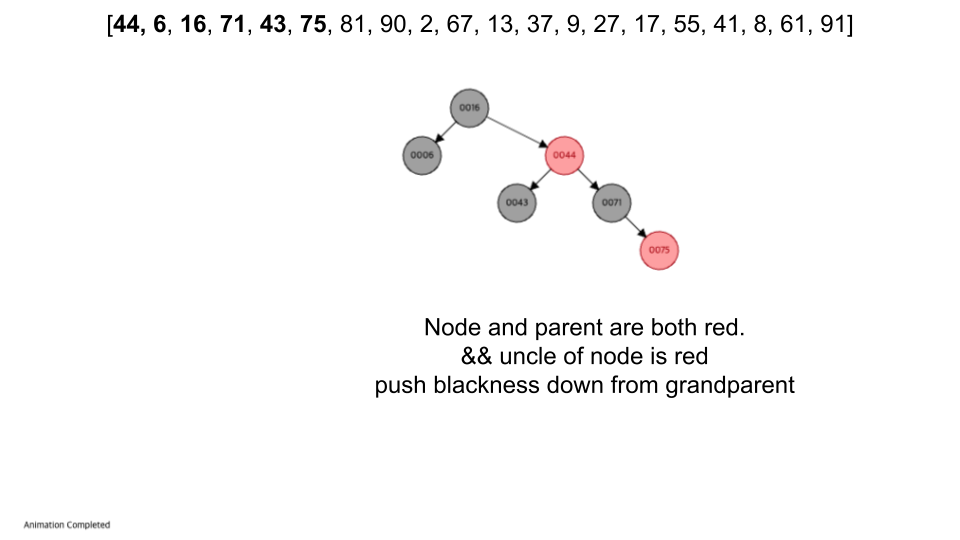
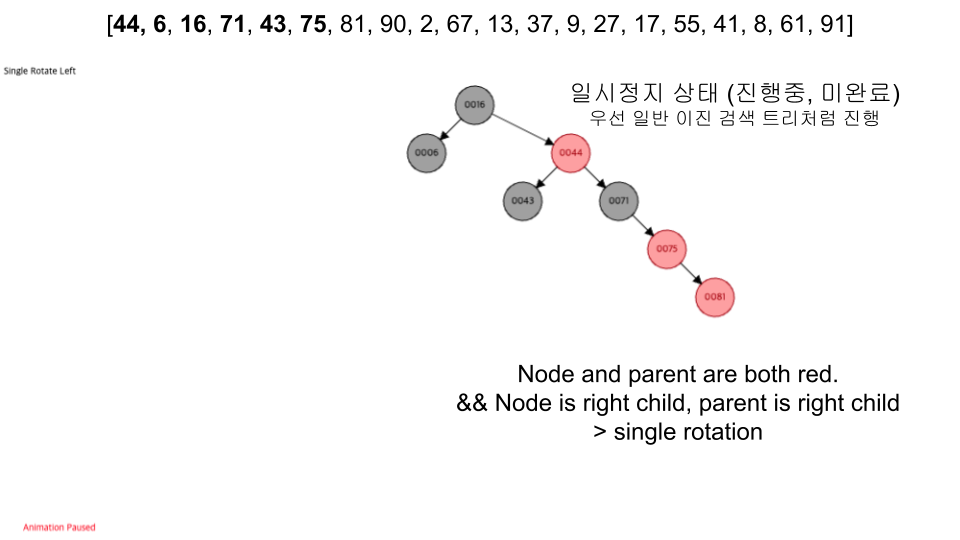
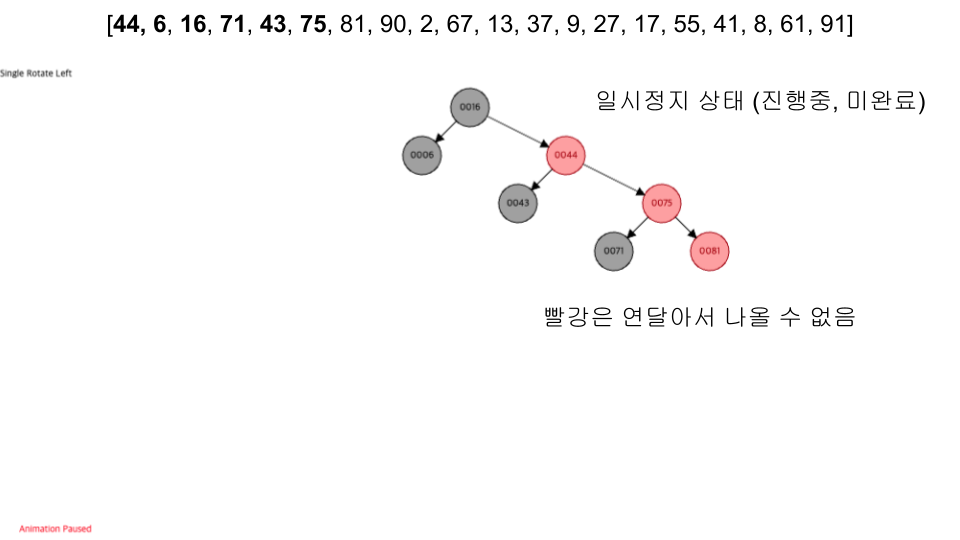
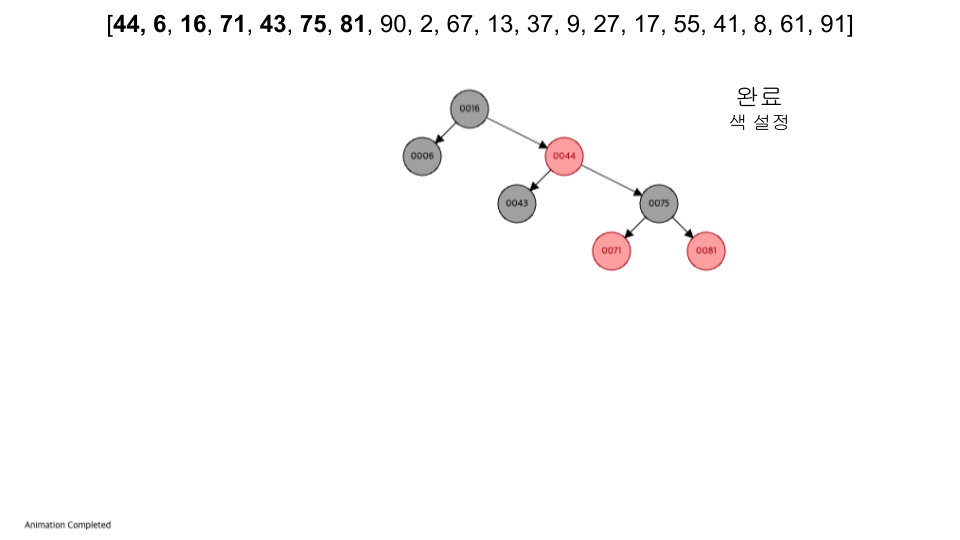
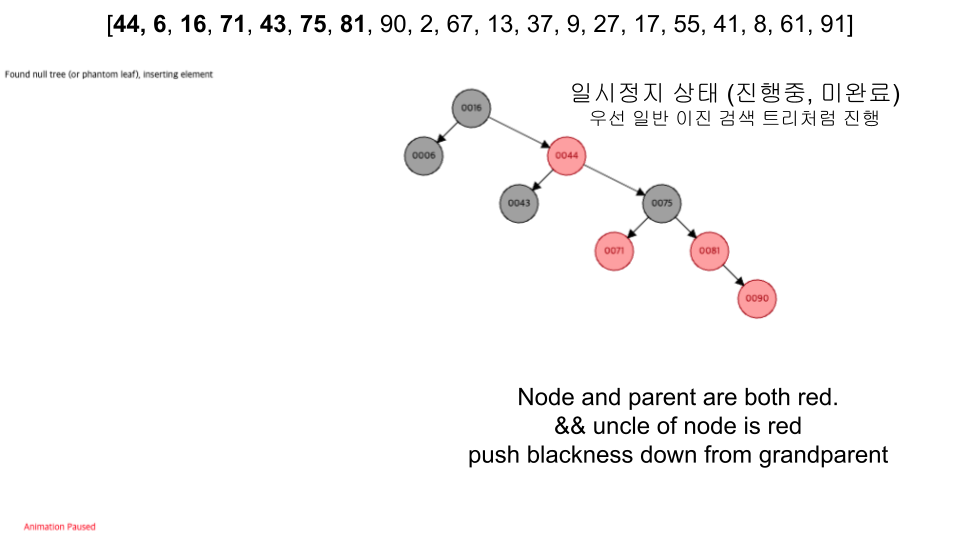
- 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
- 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다
4번, 5번 속성이 중요하다.
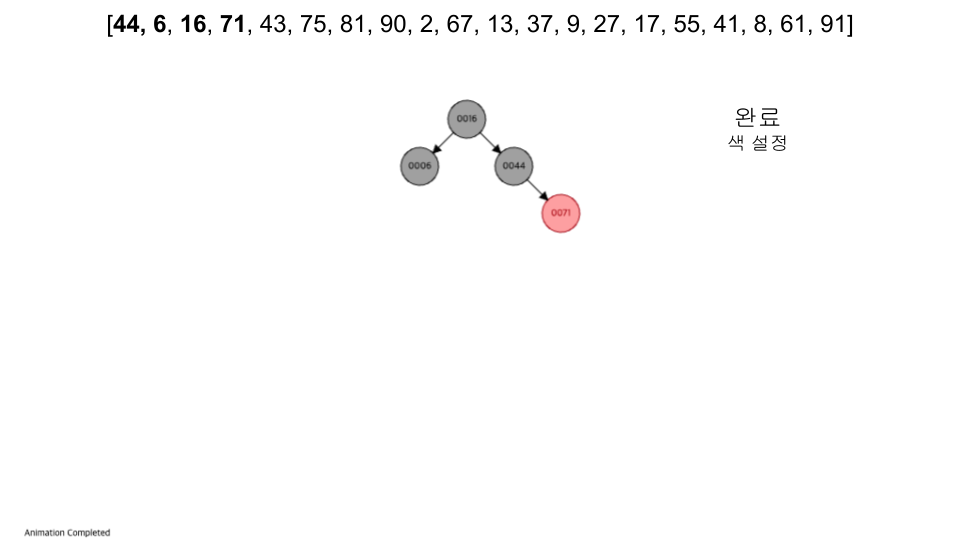
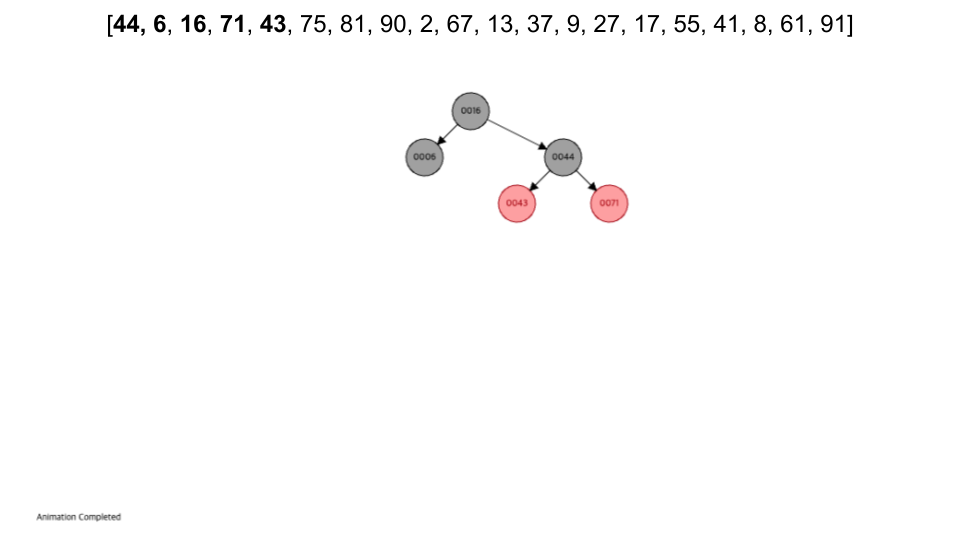
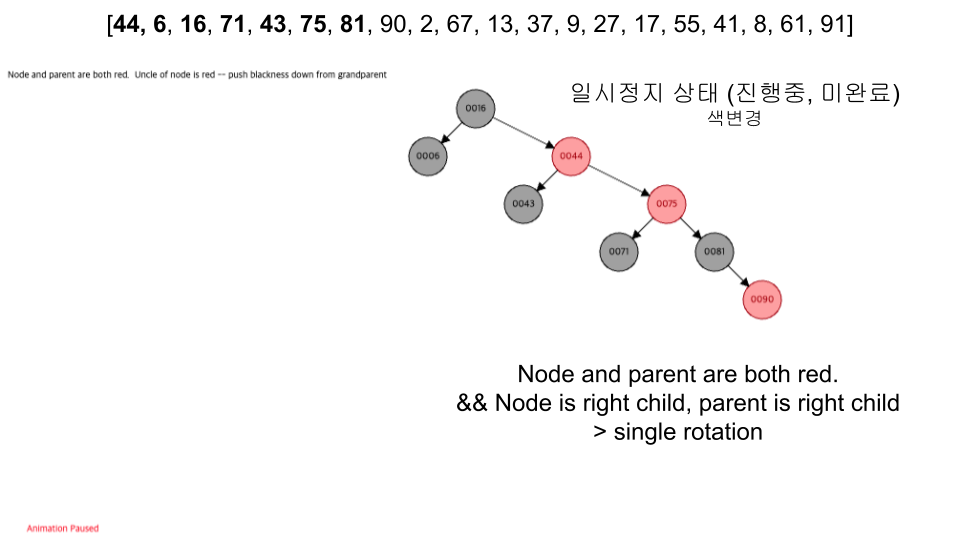
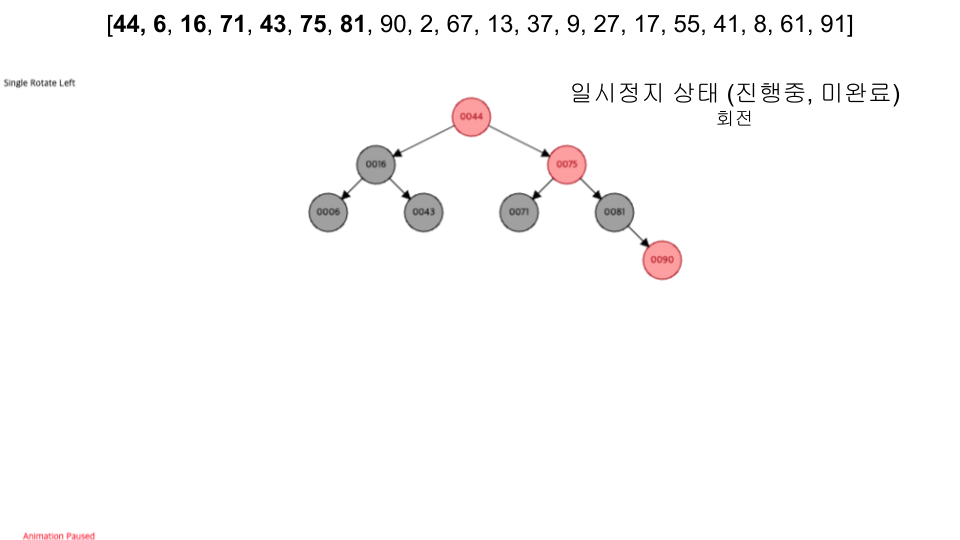
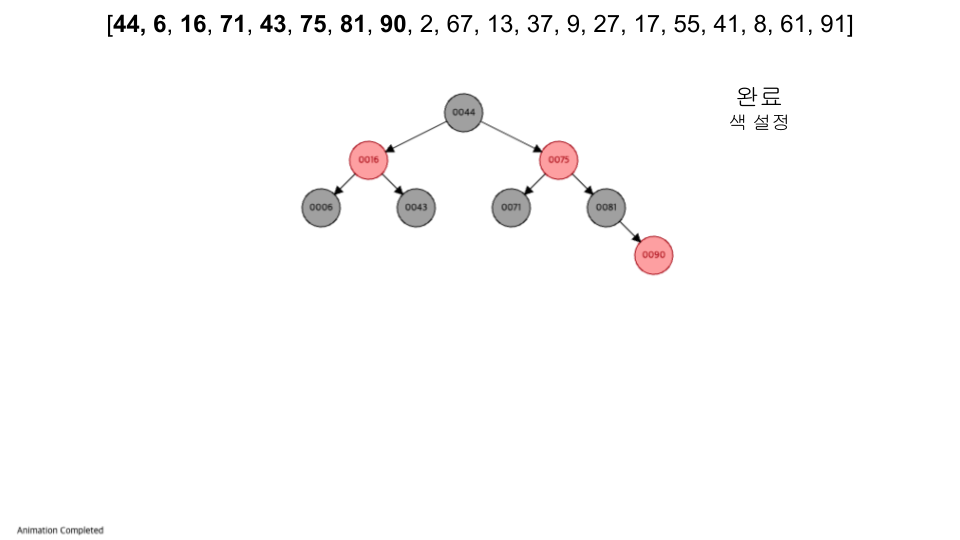
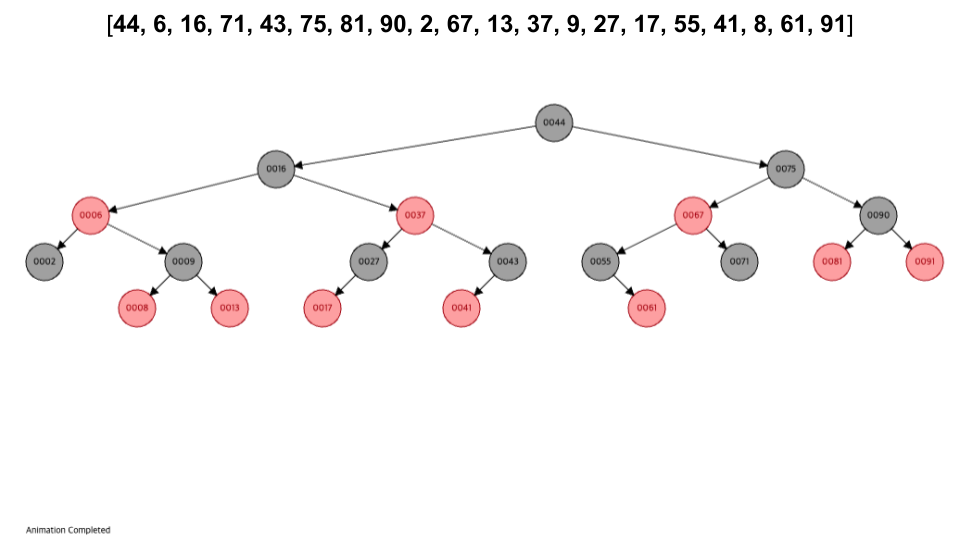
visualization
- https://www.cs.usfca.edu/~galles/visualization/RedBlack.html
- 입력 순서 :
[44, 6, 16, 71, 43, 75, 81, 90, 2, 67, 13, 37, 9, 27, 17, 55, 41, 8, 61, 91]


성능
- amortized (분할 상환 분석) 라는 개념이 사용되었는데 전반적으로 x 에 가까울 것이다 정도로 이해하면 된다고 한다.
| amortized | 최악 | |
|---|---|---|
| 조회 | O(logN) | O(logN) |
| 삽입 | O(1) | O(logN) |
| 삭제 | O(1) | O(logN) |
| 공간복잡도 | O(N) | O(N) |
